红黑树详解
红黑树是一种相当复杂的数据结构,我仔细研究并亲手实现了它,这是一个多月来阅读「算法导论」给我带来成就感最大的一次。
概述
红黑树有以下五条性质:
- 节点是红色或者黑色的。
- 根节点的黑色的。
- nil 节点时黑色的。
- 每个红节点的左子节点和右子节点必定是黑色的。
- nil 节点在任意位置黑深度都相等。
nil 节点就是空节点,在红黑树的实现中,nil 节点代替二叉树中的 NULL:叶子节点的左节点和右节点指针都指向 nil 节点;只一个子树的节点,其另外一个子节点指针也指向 nil 节点;根节点的父节点也指向 nil 节点。nil节点的父节点和右节点都是自己,左节点为红黑树的根节点。如果红黑树为空(没有根节点),那么nil节点的左节点就也是自己。nil节点的存在大大方便了很多操作。
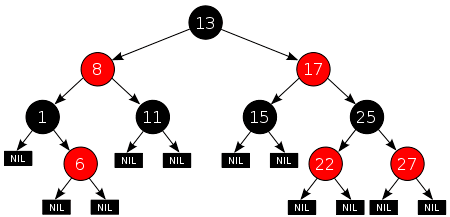
红黑树的这5条性质中,第4和第5条性质保证了红黑树是相对“平衡”的。
- 第4条保证了:两个红节点不可能直接相连。
- 第5条保证了:从 nil 节点开始,从上至下沿任意一条道路,再回到 nil 节点,经过的黑节点的数量是一样的。
这样,红黑树中的所有叶子节点到根节点的长度,在最坏情况下也不会大于最好情况下的两倍,所以红黑树就能保持「大致」的平衡。
将黑节点视为框架(骨骼),红节点视为填充物(血肉)。黑节点控制着红黑树的平衡,一棵黑高度是n的红黑树,根节点的左右子树的黑高度就都很整齐地是 n 而不会不一样,这样红黑树就不会失去平衡;红节点使红黑树能够容纳有限程度的不平衡,固定黑高度的子树,能够容纳的节点个数是有限的。
如果一棵子树中已经塞满了红节点,再试图向其中插入节点,就会导致树失去平衡,这是就要进行一些额外的处理(包括旋转根节点,将一棵子树中的节点移到另一棵子树中去)。红黑树的复杂就在于此:如何在插入节点(还有)删除节点后,保证树仍然具有上述五条性质,这其中包含一些精妙的设计。
二叉查找树部分
红黑树在二叉查找树的基础上修改而来。首先看一下节点类 node 的定义:
class node
{
public:
node (int val): value(val), isRed(true) {};
node (int val, node *le, node *ri, node *pa): value(val), left(le),
right(ri), parent(pa), isRed(true) {};
int value;
node *left;
node *right;
node *parent;
bool isRed;
};节点有四个属性,value 表示节点值,isRed 表示红色还是黑色,left,right,parent指向左子结点、右子结点和父节点,构造函数用来构造节点,节点构造出来默认是红色的。
二叉查找树的特点是,根节点左子树中的节点全部小于根节点,右子树中的节点全部大于根节点。二叉查找树的插入和删除操作都有所体现。红黑树 rbtree 类的定义如下,先看 public 部分
class rbtree
{
public:
rbtree();
void insertValue(int val);
node *searchValue(int val);
void removeValue(int val);
void removeNode(node *n);
void printTree();
private:
node *nil;
// 省略
};rbtree 类提供这样一些函数,插入一个值 insertValue ,查询一个值 searchValue ,删除一个节点 removeNode 或删除一个值 removeValue (即先查询,然后再删除查询到的第一个节点),在控制台输出树 printTree。
由于操作红黑树的函数经常用到递归,需要传入当前节点(从 nil 节点开始),所以上述函数都是通过调用 private 函数(调用这些函数是都要传入一个“当前节点”,以方便函数在当前节点的子结点上继续调用自己)来进行完成任务的:
rbtree::rbtree()
{
// 构造空的红黑树,生成nil节点,其left,right,parent都指向自己
nil = new node(0);
nil->isRed = false;
nil->left = nil->right = nil->parent = nil;
}构造函数构造一个空的红黑树,只有 nil 节点,nil 节点的左子结点还是 nil 节点自己,如果非空,则是树的根节点。
void rbtree::insertValue(int val)
{
// 从nil节点开始,插入一个值
insert(nil, val);
}insertValue 插入一个数值,它调用 insert 函数并将 nil 传递作为当前节点传入。任何插入操作都会从nil节点开始,沿着红黑树向下搜寻合适的位置。如果是空树,那就直接插在nil->left(根节点)上。
node *rbtree::searchValue(int val)
{
node *res = search(nil->left, val);
return (res == nil) ? NULL : res;
}searchValue 在红黑树中查询一个值,如果查到了,则返回查到的节点,如果没有查到,返回NULL(而不是nil,因为该函数是对外的接口,外面不知道红黑树中有一个 nil 节点这回事)。
void rbtree::removeNode(node *n)
{
remove(n);
}删除节点很简单,就是调用私有的 remove 方法。删除节点不需要从 nil 节点开始遍历,直接从待删除的节点开始操作就可以了,所以 remove 方法并不接受一个 「当前节点」参数。
void rbtree::removeValue(int val)
{
node *tn = search(nil->left, val);
if (tn == nil)
{
return;
}
else
{
removeNode(tn);
}
}删除一个值,就是先根据值查找节点,如果查到了,就删除该节点。
void rbtree::printTree()
{
// 将红黑树打印出来:如果为空,则显示一条消息;
// 如果不为空,则打印出来
if (nil->left == nil)
{
cout << "Empty Tree";
}
else
{
output(nil->left, 1, 0);
}
cout << endl;
}输出红黑树也很简单,先检查是不是空树,如果是,输出一条消息,如果不是,调用私有函数 output() 并传入根节点。
现在看一下上面用到的几个私有函数。先看声明:
class rbtree
{
public:
// 省略
private:
node *nil;
void insert(node *n, int val);
void remove(node *n);
node *search(node *n, int val);
void output(node *n, int level, int blevel);
// 省略
};几个方法的实现如下所示:
void rbtree::insert(node *n, int val)
{
// 在以节点n为根的子树中插入值val,从根部开始查找,
if (n == nil) /*从nil开始,说明是一次插入操作的第一次调用*/
{
if (nil->left != nil) /*非空树*/
{
insert(nil->left, val);
}
else /*空树*/
{
node *tn = new node(val, nil, nil, nil);
nil->left = tn;
fixInsert(tn);
}
}
else /*n为普通节点(而不是nil)*/
{
node **pos = (val < n->value) ? &(n->left) : &(n->right);
if (*pos != nil) /*待插入位置非空,需要在子树中寻找更具体的位置*/
{
insert(*pos, val);
}
else /*待插入的位置为空,将新节点插入到该位置上*/
{
node *tn = new node(val, nil, nil, n);
*pos = tn;
fixInsert(tn);
}
}
}插入操作,首先检查传入的当前节点n是不是nil节点:
- 如果是,说明是插入操作的第一次调用,传入了nil节点。检查红黑树是不是空树:
- 如果是空树,就将其作为根节点,插入在
nil->left处。 - 如果不是,就在根节点上调用自己。
- 如果是空树,就将其作为根节点,插入在
- 如果不是,就说明已经下放到普通节点了,将待插入的值与自己比较,并选择合适的位置(左子树或右子树)。检查这个合适的位置是不是空:
- 如果不是空,就在这个子节点上继续调用自己。
- 如果是空,就使用这个值构造一个新节点,插入在这个位置上。
你可能注意到,在真正插入一个节点(而不是继续调用自己)后,我们都执行了一个fixInsert(),这是这篇博文的重点之一,稍后再讲。
node *rbtree::search(node *n, int val)
{
if (n == nil)
{
return nil;
}
else if (n->value == val)
{
return n;
}
else
{
return (val < n->value) ? search(n->left, val) : search(n->right, val);
}
}查询操作相对简单,就是比较查询值和当前节点值是否相等,如果相等,就返回当前节点,否则,就根据查询值与当前值的大小关系,在左子树或右子树中继续查询。
void rbtree::remove(node *n)
{
// 如果有两个非空子树,就将待删除节点与左子树中最大节点交换值,
// 然后删除左子树中的那个“最大节点”
if (n->left != nil && n->right != nil)
{
node *target = n->right;
while (target->left != nil)
{
target = target->left;
}
switchValue(n, target);
remove(target);
}
else /*至少有一个子树为空*/
{
node *c = (n->left == nil) ? n->right : n->left;
(*getSelfFromParent(n)) = c;
if (c != nil)
{
c->parent = n->parent;
}
// 如果删掉的是红节点,什么都不做
if (n->isRed == true)
{
return;
}
// 如果删除的节点是黑色,而删除节点的子节点是红色,那就将子节点染黑
if (c->isRed == true)
{
c->isRed = false;
}
else
{
// 如果删除节点是黑色,删除节点的子节点也是黑色,麻烦来了
fixRemove(c, c->parent);
}
}
}删除操作,稍微复杂一些。二叉查找树中删除一个节点是这样的。
- 如果待删除的节点没有子节点或者只有一个子节点,那就直接将其删除,将子节点(如果有的话)代替自己接在父节点上。
- 如果待删除的节点有两个子节点(就是有两个非空子树),那就将该节点和左子树中的最大节点交换节点值,然后将左子树中的最大节点删除(该节点既然是左子树中的最大节点,就不可能有右子结点,所以不会有两个非空子树)。而且,左子树中的最大节点,一定比左子树中的其余所有节点都大(因为它是最大节点),又比右子树中的所有节点都小(它在左子树中),所以让该节点坐在原来待删除节点的位置上,不会破坏二叉查找树的属性。
你可能注意到,在真正删除一个节点后,在某些特定条件下,我们需要进行一些额外的处理,甚至调用 fixRemove() 函数。这是本篇博文的另一个重点,将在后面详细解释。
void rbtree::output(node *n, int level, int blevel)
{
if (n == nil)
{
return;
}
int tb = (n->isRed) ? 0 : 1;
output(n->left, level + 1, blevel + tb);
for (int i = 1; i < level; i++)
{
cout << " ";
}
cout << n->value << ((n->isRed) ? "R" : "");
if (n->left == nil || n->right == nil)
{
cout << "(" << blevel + tb << ")";
}
cout << endl;
output(n->right, level + 1, blevel + tb);
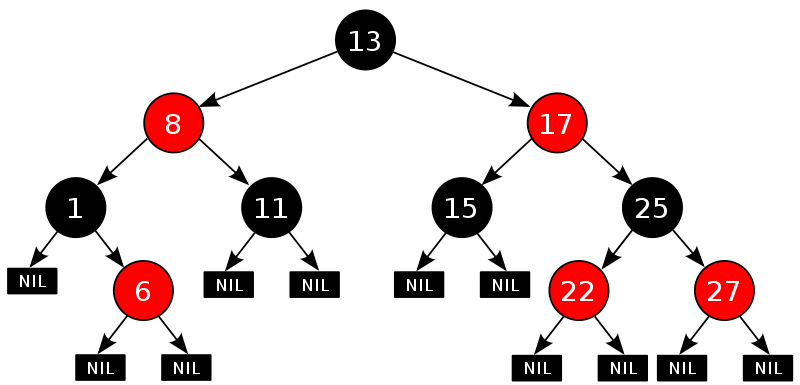
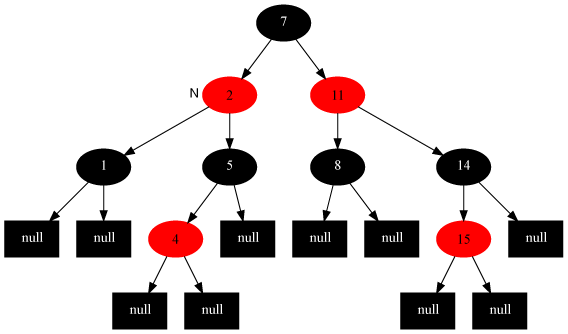
}输出一个子树,传入的是当前节点,其深度与黑深度。printTree()函数调用该函数。该函数负责控制缩进,体现节点的深度;负责用字符R标记红节点,还负责输出叶子节点的黑深度。如下就是一个简单地五个元素的红黑树的输出。
>> g++ rbtree.cpp
>> ./a.out
5(2)
8R(2)
10
15R(2)
17(2)
>>红节点打上了字符R标记,而且所有具有指向nil节点指针的节点的黑深度也输出在括号中(本例中为2)。
旋转
为了进行 fixInsert() 和 fixRemove() ,我们定义旋转操作还有一些其他的辅助函数。先看类中的函数声明:
class rbtree
{
public:
// 省略
private:
// 省略
bool rotateLeft(node *n);
bool rotateRight(node *n);
node **getSelfFromParent(node *n);
node **getSiblingFromParent(node *n);
void switchColor(node *n1, node *n2);
void switchValue(node *n1, node *n2);
bool isLeft(node *n);
// 省略
};它们的实现如下所示:
bool rbtree::rotateLeft(node *n)
{
if (n->right == nil)
{
return false;
}
else
{
node *x = n;
node *y = n->right;
node *p = y->left;
(*getSelfFromParent(x)) = y;
y->parent = x->parent;
y->left = x;
x->parent = y;
x->right = p;
if (p != nil)
{
p->parent = x;
}
return true;
}
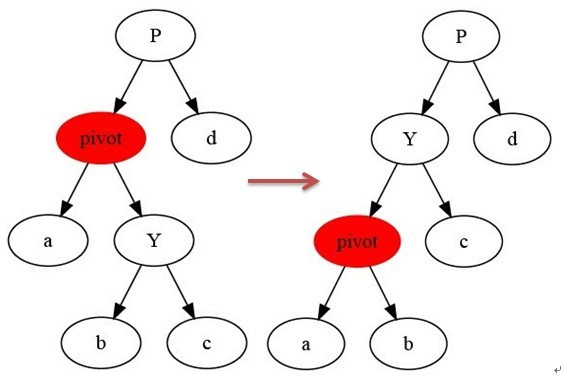
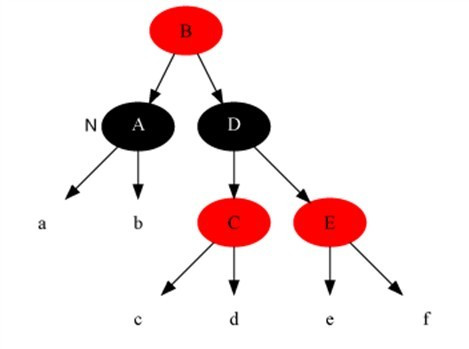
}rotateLeft 左旋节点n。左旋的示意图如下所示:节点X左旋之后,由X的右子节点Y代替X成为X的父亲的子节点,X成为Y的左子结点,原先Y的左子结点成为了X的右子结点。旋转后,Y占据了X的位置,原先该位置上的左子树和右子树中的节点个数得到了调整,左子树中新加入了X节点,右子树中去除了Y节点,而β子树也离开了右子树,转到左子树中。实际上,红黑树就是通过这种调整来保持本身的大致平衡的。

bool rbtree::rotateRight(node *n)
{
if (n->left == nil)
{
return false;
}
else
{
node *y = n;
node *x = y->left;
node *p = x->right;
(*getSelfFromParent(y)) = x;
x->parent = y->parent;
x->right = y;
y->parent = x;
y->left = p;
if (p != nil)
{
p->parent = y;
}
return true;
}
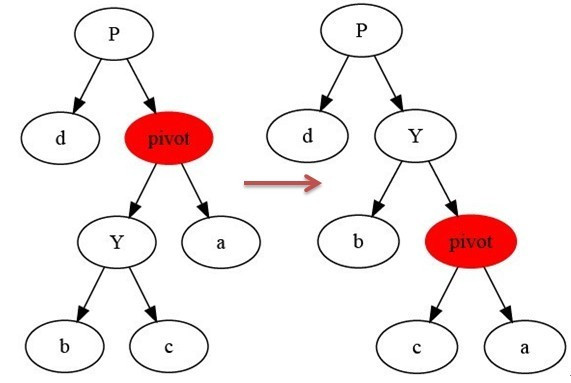
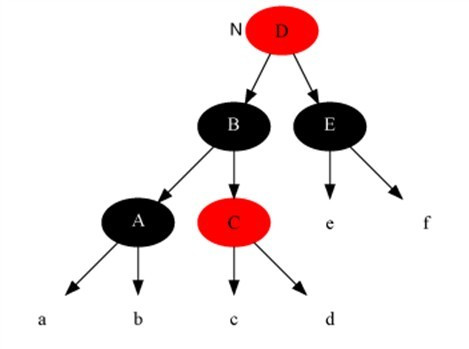
}右旋与左旋对称。
还有一些其他的辅助函数,可以使后面修复插入和删除的逻辑代码更加易读:
node **rbtree::getSelfFromParent(node *n)
{
node *p = n->parent;
return p->left == n ? (&(p->left)) : (&(p->right));
}
node **rbtree::getSiblingFromParent(node *n)
{
node *p = n->parent;
return p->left == n ? (&(p->right)) : (&(p->left));
}getSelfFromParent 和 getSiblingFromParent 函数分别获取一个指针,该指针指向父节点中指向自己的指针和指向兄弟的指针。函数返回的是指针的指针,而不是直接指向自己或兄弟的指针,是因为这样可以用来改变指向的指针所指的内容。比如,*getSelfFromParent(n1)=n2 就可以将节点n1的父亲节点中,指向n1的指针(left 或 right)改成指向n2。
bool rbtree::isLeft(node *n)
{
// 判断节点是否为父节点的左子结点
return n->parent->left == n;
}
void rbtree::switchColor(node *n1, node *n2)
{
bool tmp = n1->isRed;
n1->isRed = n2->isRed;
n2->isRed = tmp;
}
void rbtree::switchValue(node *n1, node *n2)
{
int tmp = n1->value;
n1->value = n2->value;
n2->value = tmp;
}这三个函数都比较简单实用,isLeft() 函数用来判断某个节点它是父亲的左子结点还是右子结点,switchColor() 函数用来交换两个节点的颜色,switchValue 用来交换两个节点的值。
修复插入
交代了这么多,总算进入重点了。
那么,为什么要修复插入呢?之前说到,在插入一个节点之后,我们执行 fixInsert() 。实际上,新插入了节点,该节点可能会破坏红黑树的性质1或5。
我们知道,新插入的节点n是红色的:
- 如果n的父节点p是黑色的
- 如果p是nil(也就是说,n是根节点),那么将n染成黑色,插入完成了(case1)。
- 如果p不是nil,而那么什么也不用做,插入就完成了(case2)。——如果它的父亲在插入前是叶子节点,那么插入之后n成为叶子节点,n本身是红色的,所以它的黑深度和p一样。如果在插入之前,p就有一个子节点s,那么s一定是红色的叶子节点(如果s是黑色的,而p的另一个子树为空,就违反了性质5),n插入之后,s就是n的兄弟节点。s和n都会具有与p一致的黑深度,也不会破坏性质。
- 如果n的父节点p是红色的,再插入一个红色子节点就违反了性质4,所以需要进行处理:
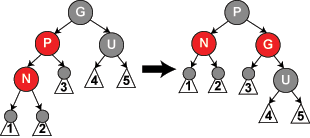
- 如果n的叔叔u是红色的,那么将u和p染成黑色,将n的爷爷节点g染成红色,然后执行
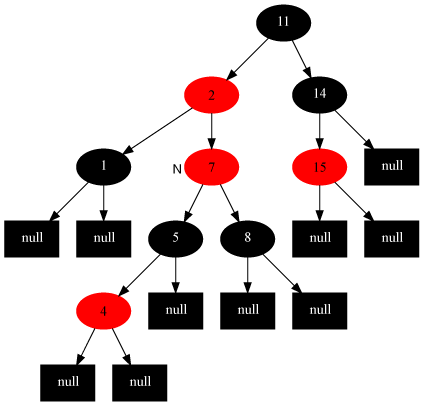
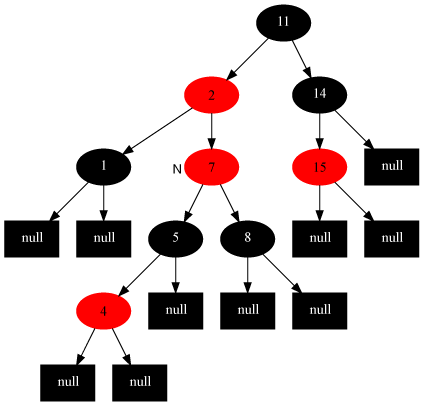
fixInsert(g)(case3)。——如图所示,叔叔u是红色的,爷爷g一定是黑色的。这是p和n是连续的红节点,违反了性质4。处理之后,g变成了红色,又有可能违反性质4(g的父节点又是红色的)或者性质1(g就是根节点了)。这是再次对g调用fixInsert()。 - 如果n的叔叔u是黑色:
- 如果n为左子节点且p为左子节点(如图) / n为右子节点且p为右子结点(与图对称),那么右旋/左旋g并交换p和g的颜色(case3)。
- 如果n为右子结点且p为左子结点(如图) / n为左子结点且p为右子结点(与图对称),那么左旋/右旋p转化为上述情形(case4)。
- 如果n的叔叔u是红色的,那么将u和p染成黑色,将n的爷爷节点g染成红色,然后执行
修复插入case1:

修复插入case2:

修复插入case3:
代码如下所示:
void rbtree::fixInsert(node *n)
{
if (n->parent == nil)
{
fixInsertCase1(n);
return;
}
// 父节点P为黑色,则什么都不做
if (n->parent->isRed == false)
{
fixInsertCase2(n);
}
else // 父节点P为红色
{
node *p = n->parent;
node *u = *getSiblingFromParent(p);
if (u->isRed == true) /*叔叔节点U为红色*/
{
fixInsertCase3(n);
}
else /*叔叔节点U为黑色*/
{
fixInsertCase4(n);
}
}
}
void rbtree::fixInsertCase1(node *n)
{
n->isRed = false;
}
void rbtree::fixInsertCase2(node *n)
{
return;
}
void rbtree::fixInsertCase3(node *n)
{
node *p = n->parent;
node *u = *getSiblingFromParent(p);
node *g = p->parent;
p->isRed = u->isRed = false;
g->isRed = true;
fixInsert(g);
}
void rbtree::fixInsertCase4(node *n)
{
node *p = n->parent;
node *u = *getSiblingFromParent(p);
node *g = p->parent;
if (isLeft(n) && isLeft(p))
{
rotateRight(g);
switchColor(p, g);
}
else if (!isLeft(n) && !isLeft(p))
{
rotateLeft(g);
switchColor(p, g);
}
else if (!isLeft(n) && isLeft(p))
{
rotateLeft(p);
rotateRight(g);
switchColor(n, g);
}
else // isLeft(n) && !isLeft(p)
{
rotateRight(p);
rotateLeft(g);
switchColor(n, g);
}
}修复删除
按照二叉查找树的删除方法,删除节点的操作都能转化为删除至多具有一个子节点的节点。如果被删除节点是红色的,那肯定不会对红黑树的性质造成影响,所以,完全不用在意。我们在意的是被删除节点是黑色的情况:如果被删除节点的子节点是红色的,那也好办,将子节点直接染黑就行,因为子节点代替了被删除节点的位置,它原来是红色的,对黑深度就没有贡献,染黑它,就可以起到被删除节点的作用。
最难办的是,如果被删除节点是黑色的,而且他的子节点还是黑色的(其实这时子节点只能是nil节点了),这时这条路径上就少了一个黑节点,此时就需要调用 fixRemove() 来修复。实际上,调用该函数的时机是,某一个节点由于某种变化(这里就是删除了一个黑节点且接上来的子节点也是黑色),导致通过该节点的路径少了一个黑节点。
fixRemove() 的逻辑是这样的(实际上,第一次删除节点后,节点的子节点n都是 nil ,只有开始递归调用自己之后,n才是正常的节点):
- 如果被删除节点的子节点n就是根节点(case1),那么结束。
- 如果n不是根节点:
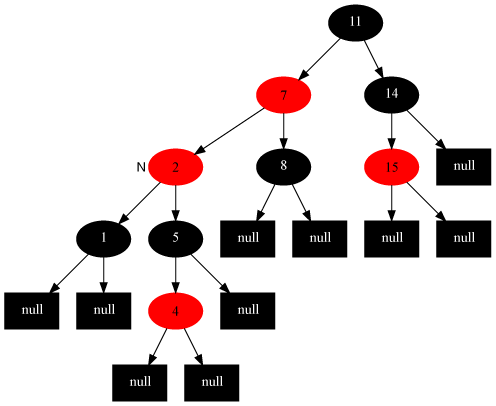
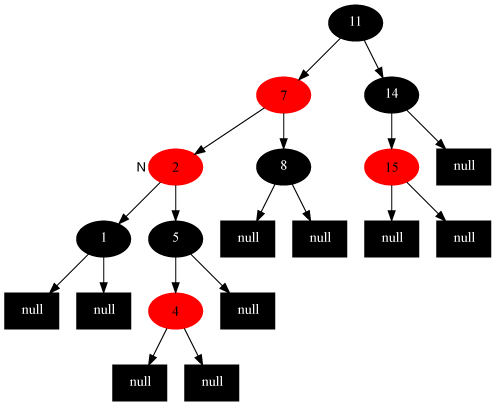
- n的兄弟节点s是红节点(case2),那么N的父节点p和s互换颜色,并左旋(如图)/右旋(与图对称)p,转入case4,case5或case6。
- n的兄弟节点s为黑节点,s的左右节点都是黑节点(case3),那就将s染成红色,再对p执行
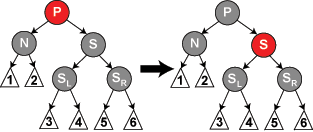
fixRemove()。将s染成红色导致所有通过s的路径少了一个黑节点,这样就与通过n的路径一致了。现在通过p节点的所有路径都少了一个黑节点,所以要继续对p做fixRemove()。 - s与s的两个子节点都是黑色,但是p是红色(case4)。这时只需要交换p和s的颜色即可。原先通过p的路径上的黑节点数目没有变,但是通过n的节点数目补回来了。
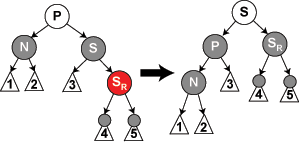
- n是左节点(否则对称)的情况下,s是黑,s的左子节点是红,右子结点是黑(case5)。这时右旋s,这样n就有了一个右子节点为红色的兄弟,转入case6。
- n是左节点(否则对称)的情况下,s是黑,s的右子节点是红(case6)。这时左旋p,然后交换s和p的颜色,并且将是s的右节点染黑。这样,不管p原先是红色还是黑色,通过n的路径都增加了一个黑节点,而通过sr的路径保持不变。
修复删除case2:

修复删除case3:

修复删除case4:
修复删除case5:

修复删除case6:
代码如下所示:
void rbtree::fixRemove(node *n, node *p)
{
if (p == nil)
{
fixRemoveCase1(n, p);
return;
}
node *s = *getSiblingFromParent(n);
if (s->isRed == true)
{
fixRemoveCase2(n, p);
return;
}
// s为黑色
if (p->isRed == false && s->left->isRed == false && s->right->isRed == false)
{
fixRemoveCase3(n, p);
return;
}
if (p->isRed == true && s->left->isRed == false && s->right->isRed == false)
{
fixRemoveCase4(n, p);
return;
}
if ((isLeft(n) && s->left->isRed == true && s->right->isRed == false) ||
(!isLeft(n) && s->right->isRed == true && s->left->isRed == false))
{
fixRemoveCase5(n, p);
return;
}
if ((isLeft(n) && s->right->isRed == true) ||
(!isLeft(n) && s->left->isRed == true))
{
fixRemoveCase6(n, p);
}
}
void rbtree::fixRemoveCase1(node *n, node *p)
{
return;
}
void rbtree::fixRemoveCase2(node *n, node *p)
{
node *s = *getSiblingFromParent(n);
if (isLeft(n))
{
rotateLeft(p);
}
else
{
rotateRight(p);
}
switchColor(p, s);
fixRemove(n, p);
}
void rbtree::fixRemoveCase3(node *n, node *p)
{
node *s = *getSiblingFromParent(n);
s->isRed = true;
fixRemove(p, p->parent);
}
void rbtree::fixRemoveCase4(node *n, node *p)
{
node *s = *getSiblingFromParent(n);
switchColor(s, p);
}
void rbtree::fixRemoveCase5(node *n, node *p)
{
node *s = *getSiblingFromParent(n);
if (isLeft(n))
{
rotateRight(s);
}
else
{
rotateLeft(s);
}
fixRemove(n, p);
}
void rbtree::fixRemoveCase6(node *n, node *p)
{
node *s = *getSiblingFromParent(n);
if (isLeft(n))
{
s->right->isRed = false;
rotateLeft(p);
}
else
{
s->left->isRed = false;
rotateRight(p);
}
switchColor(p, s);
}这样就实现了红黑树。